DÍA MUNDIAL DEL NÚMERO PI

Hoy 14 de Marzo se celebra el "Día Mundial del número PI", debido a que en inglés la fecha se suele poner mes-día, así sería 3-14 (Marzo-14).

Si quieres enterarte un poco más puede leer un artículo muy interesante de Rafael Bachiller que es astrónomo, director del Observatorio Astronómico Nacional (IGN) y miembro del Consejo Editorial de EL MUNDO.

Aplicación de Trigonometría: "Círculo Unitario"

La aplicación para móvil "Círculo unitario" te puede ayudar a entender mejor las razones trigonométricas de cualquier ángulo, en especial para los alumnos de 4º de E.S.O. y 1º de Bachillerato.

Trabaja con la circunferencia goniométrica

Con el dedo eliges el ángulo y automáticamente la aplicación nos da el valor de las proyecciones, es decir el valor del seno, coseno y tangente de ese ángulo elegido.

También es útil para el estudio de funciones trigonométricas

Día del mol

 Se celebra el 23 de octubre entre las 6:02 AM y las 6:02 PM, haciendo referencia al número de Avogadro (aproximadamente, 6,02 ⋅ 10²³, que es el número de partículas que hay en un mol).

En este día tan especial se pretende despertar el interés por la belleza de los números y de sus aplicaciones en la ciencia.

Si quieres tener claro lo que es un mol puedes ver el siguiente vídeo:

Calculadora & Móvil

 Cada vez usamos más nuestros móviles como calculadora.

Os muestro una foto con un ejemplo claro de lo que puede pasar si no tenemos el control sobre la tecnología.

Como puedes ver la misma operación se interpreta de forma diferente.

Si seguimos las prioridades de las operaciones de forma correcta tenemos que hacer primero el paréntesis: 6:2·3,

y a continuación como solo quedan multiplicaciones y divisiones las haremos de izquierda a derecha: 3·3 =9

Es decir el móvil ha ganado a la calculadora.

La calculadora interpreta que tiene que hacer también primero el paréntesis: 6:2·3

pero a continuación hace las multiplicaciones y divisiones de derecha a izquierda: 6:6=1, lo que no es correcto.

Tenemos que conocer bien nuestro móvil y nuestra calculadora para asegurarnos de que se siguen bien las prioridades a la hora de hacer las operaciones.

Modelos matemáticos que ayudan a estudiar sistemas complejos

La realidad suele ser muy compleja y depender de muchas variables, los investigadores pueden identificar qué variables son las más importantes y hacer teorías y modelos matemáticos que se comporten como en la realidad.

Así desde hace muchos años hemos ido obteniendo fórmulas matemáticas que son capaces de  predecir lo que va a ocurrir a partir de una situación inicial.

Algunas de esas fórmulas matemáticas las vamos estudiando en nuestras clases de física y química, o de ciencias en general.
Una investigación básica de un físico sobre el movimiento de dispersión de un conjunto de partículas se puede aplicar unos años más tarde por un sociólogo para estudiar los movimientos migratorios o la forma en la que un grupo de personas se mueve por un recinto cerrado como una feria o un evento deportivo, incluso por un especialista médico (epidemiólogo) para estudiar cómo evoluciona el contagio por un virus como el que nos tiene paralizados en estos días.

Se han hecho modelos matemáticos con los que entender cómo evoluciona el número de personas sanas, infectadas y curadas en una población concreta.

Un ejemplo es el artículo "Por qué brotes como el del coronavirus crecen exponencialmente y cómo aplanar la curva" de Harry Stevens en el Washinton Post, muy intuitivo y fácil de entender.

Si lo visitas puedes ver un modelo con cuatro situaciones diferentes, así podrás entender mejor el por qué de las medidas sanitarias impuestas a la población española (y también en otros países afectados).

Es responsabilidad de todos frenar el contagio y conseguir que el sistema sanitario no se sature. 

QUÉDATE EN CASA!!!

(por unos pocos días y así saldremos todos antes)

Aplicación Mathway

Mathway es un editor matemático online que permite resolver problemas matemáticos de muy diverso tipo: matemáticas básicas, álgebra, geometría, trigonometría, cálculo, estadística, etc.
Una vez se introducen los datos automáticamente, nos ofrece la solución así como pasos intermedios, gráficos e imágenes en algunos casos.

Puedes trabajar desde tu ordenador, o descargarte la aplicación para tu móvil (Android o Apple)

Para los cálculos básicos es muy intuitivo y fácil de utilizar. Pero para algunas funciones más avanzadas no lo es tanto y la ayuda no es muy buena que digamos...

Aplicación xGraphing

Si quieres manejar gráficas de funciones con tu móvil puedes descargarte de forma gratuita la aplicación xGraphing (9MB)

De forma sencilla podrás dibujar toda clase de funciones matemáticas a partir de su expresión algebraica o simplemente conociendo alguno de sus puntos.

También si conoces alguno de los puntos de la gráfica podrás obtener su expresión algebraica.

DÍA ESCOLAR DE LAS MATEMÁTICAS 12 de MAYO

En el 2000 se celebró el Año Mundial de las Matemáticas, un acontecimiento internacional declarado por la UNESCO en el que se eligió el 12 de mayo como fecha del calendario escolar dedicada a la difusión de las ciencias matemáticas en los centros educativos, en honor al matemático español Pedro Puig Adam.
Si quieres saber mejor lo que hacen los matemáticos puedes ver el siguiente vídeo.

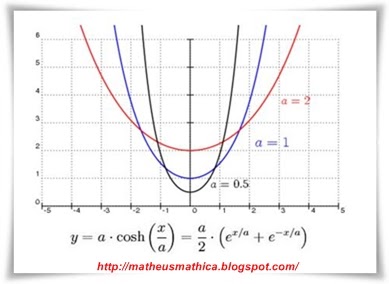
El Número e

El número e es irracional como también lo son el número pi, el número de oro o la raíz cuadrada de 2. Fué descubierto por el matemático escocés John Napier (1550-1617) conocido por ser el primero en definir los logaritmos.
El número e tiene gran cantidad de aplicaciones, tanto en cálculo matemático como en diversas aplicaciones a otras ciencias (físicas, químicas, geológicas, etc)

Un ejemplo de aplicación del número e es la catenaria.

Una cuerda pesada, flexible, inextendible y suspendida de dos puntos toma la forma de la catenaria. Esta catenaria es una curva plana cuya ecuación empleando coordenadas cartesianas (contenidas en el plano de la curva) y escogidas de manera que el eje Y coincida con el mínimo de la curva, resulta ser:

Para saber más en la wikipedia...

FELIZ NAVIDAD !!!

Una forma original de felicitar las Navidades es a través de mensajes matemáticos, ahí van unos cuantos...

... y seguro que vosotros conocéis alguno más.

Aplicación Photomath

El avance de la tecnología es impresionante, hace unos diez años sería ciencia ficción, pero hoy es realidad. Photomath es una aplicación para móviles que con sólo apuntar tu cámara a una operación matemática o a una ecuación, será capaz de calcular o de resolver la ecuación.

La he probado con números enteros, decimales, fracciones, logaritmos, factorizaciones, ecuaciones de primer y segundo grado, inecuaciones de primer y segundo grado con una sola incógnita, integrales...

y funciona perfectamente, da la solución exacta en forma de fracción, raíz o logaritmo.

Además no sólo da la solución en las ecuaciones, también las resuelve paso a paso... INCREIBLE!!

Puedes utilizar esta aplicación para comprobar tus ejercicios después de hacerlos tu mismo o para darte una ayuda si estás bloqueado.

TABLAS DE MULTIPLICAR

Tanto esfuerzo para aprender las tablas de multiplicar y resulta que podíamos multiplicar usando nuestras manos o dibujando.
Puedes comprobarlo en los siguientes vídeos.

• Tablas de 6 al 10 

• Tabla del 9

• Dibujando rectas y contando puntos

Vídeos de matemáticas

En los siguientes vídeos podrás descubrir curiosidades y aplicaciones de las matemáticas:

Imágenes sacadas de TVE1, en el que se da una visión rápida de la aplicación de las matemáticas.

"Universo Matemático" es una colección de pequeños documentales relacionados con famosos matemáticos y su contribución al mundo, aquí puedes ver el primer capítulo. Puedes acceder al resto de capítulos desde la pestaña del enlace  UNIVERSO MATEMÁTICO de este blog.

PITÁGORAS, MUCHO MÁS QUE UN TEOREMA (Universo Matemático 1)

MAS POR MENOS es otra colección de vídeos elaborados por TVE, muy divulgativos y amenos.

Aquí puedes ver un capítulo sobre FRACTALES,

Aplicación My Script Calculator

Os presento la herramienta "My Script Calculator" para móvil, tablet u ordenador, que podéis utilizar para realizar cálculos, hacer gráficas escribir expresiones matemáticas para vuestros apuntes y trabajos.
El siguiente vídeo os muestra algunas de las utilidades en la versión para móviles.

En la versión para ordenador se pueden hacer gráficas y muchas más cosas.

Los Números de 3 Cifras y el Número 1089

Escríbase un número de tres cifras, la primera y la última diferentes, por ejemplo, 825; inviértase el orden de las cifras, 528, y luego efectúese la resta de esos dos números: 825 – 528 = 297.
Agréguese a esta diferencia el número que resulta de invertir sus cifras: 297 + 792 = 1089. Se tendrá siempre el mismo número, 1089.

Para explicar este resultado, sean a, b, c las cifras de las centenas, decenas y unidades simples, respectivamente, y supongamos sea a mayor que c; tendremos:
El número elegido es 100a + 10b + c.
El número invertido es 100c + 10b + a.
Restando del primer número el segundo, tenemos:

100(a – c) + c – a,

que puede escribirse así:

100 (a – c – 1) + 90 + (10 + c – a)

El número invertido será, pues:

100 (10 + c – a) + 90 + (a – c – 1)

y sumando estas dos últimas expresiones, resulta:

100 (10 – 1) + 90 + 90 + 10 – 1 = 1089

Cálculo mental

Practica el CALCULO MENTAL en estos enlaces.

DIVISIÓN- MULTIPLICACIÓN-FACTORIZACIÓN

SUMAS-RESTAS-MULTIPLICACIONES-DIVISIONES

Fracciones para repasar

En esta web puedes repasar las FRACCIONES desde lo más básico.

Número Áureo y la Sucesión de Fibonacchi

El número de oro se encuentra en sitios que ni te imaginas, puedes hacerte a una idea si ves el siguiente vídeo.

Si quieres ampliar conocimientos lee el trabajo realizado por Margarita Rodríguez Fernández.